Articulo de MCU
Movimiento Circular Uniforme
Que es mcu
Es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto
implica que recorra
ángulos iguales en tiempos iguales. El vector velocidad no cambia el módulo pero si
dirección (es tangente
en cada punto a la trayectoria). Esto significa que solo hay aceleración normal en lugar de
aceleración tangencial o
aceleración angular.
Estas son algunas características del Movimiento Circular Uniforme:
- La velocidad es constante.
- El vector velocidad es perpendicular a la trayectoria en cada punto y su sentido es el que lleva el movimiento. Esto implica que el movimiento tiene una aceleración normal.
- Debido a que la velocidad o aceleración (módulo del vector velocidad) es constante, tanto la aceleración angular como la tangencial son cero.
- Hay un período (T), que es el tiempo que el cuerpo tarda en dar una vuelta completa. Esto implica que las características del movimiento son las mismas cada T segundos.
Convierte cualquier PDF en respuestas inteligentes.
SEUXSube tu documento. Pregunta. Entiende todo en segundos.
Analizar mi PDF gratisIndice
Fórmulas despejadas del Movimiento Circular Uniforme (MCU)
Fórmulas angulares
θ = ω * t
ω =
t =
Fórmulas tangenciales
L = v * t
v =
t =
Formulas adicionales
T =
=
f =
=
v = ω * R
L = θ * R
θ: desplazamiento angular (rad).
ω: rapidez angular (rad/s).
t: tiempo (s).
L: longitud de arco (m).
v: velocidad tangencial (m/s).
R: radio de giro (m).
T : período (s), tiempo empleado para dar una vuelta completa.
f: frecuencia (Hz), es el número de vueltas por unidad de tiempo que da un cuerpo.
Gráficas de MCU
Un cuerpo se mueve de manera circular y uniforme (m.c.u.) cuando su velocidad
angular es constante y su trayectoria es
circular. En esta sección, veremos los siguientes gráficos:
Posición
El gráfico de posición angular y tiempo de un movimiento circular uniforme (m.c.u.).
representa el tiempo en el eje
horizontal (eje x) y la posición angular en el eje vertical. La posición angular, medida en
radianes según las unidades
del Sistema Internacional (S.I.), aumenta (o disminuye) uniformemente a lo largo del tiempo.
La ecuación de la posición de un cuerpo en el instante t es la siguiente:
φ(t) = φ0 + ω * t
siendo φ0 la posición inicial, ω la velocidad
angular,
y la t el tiempo.
Velocidad
La velocidad angular, medida en radianes por segundo (rad/s) de acuerdo con el Sistema
Internacional de Unidades (S.I.),
se mantiene constante en el tiempo, como lo muestra el gráfico velocidad angular-tiempo de
un movimiento circular
uniforme (m.c.u.).
La gráfica de velocidad angular en base al tiempo se expresa con la siguiente ecuación:
ω = ω0 = cte
donde ω0 es la velocidad angular inicial, cte es
constante.
Aceleración
La aceleración en MCU es nula, siendo representado en el plano cartesiano como 0 o -0.
a = 0
Ejemplos de Movimiento Circular Uniforme
A continuación se podrá ver ejemplos clásicos del Movimiento Circular Uniforme teniendo
en cuenta
que todos estos escenarios son en un mundo ideal donde la fricción no afecta el movimiento, asi
haciendo hincapié en la velocidad es constante y la aceleración es nula.
Ejemplo 1
Las turbinas de una avión comercial giran con una velocidad constante de 60 rad/s se sabe que para completar el recorrido le toma 30 minutos. Calcular el angulo batido por la turbina del avión.

Solución:
El problema nos habla de la turbina de un avión con velocidad constante de
60 rad/s y que para completar el recorrido le toma un tiempo
de 30 minutos.
Organizando los datos tenemos lo siguiente:
Velocidad angular= 60 rad/s
tiempo = 30 * 60 = 1800 seg
Ya teniendo los datos organizados, el problema nos pide calcular el angulo que recorre en 30 minutos,
para eso buscaremos una formula en la sección de formulas que
permita calcular el angulo.
Usaremos la siguiente formula:
θ = ω * t
θ = 60 * 1800 = 108000 rad
Rta: Las turbinas del avión baten un angulo de 108000 rad en 30 minutos.
Ejemplo 2
Un atleta que practica la disciplina de lanzamiento de martillo el cual realiza el lanzamiento de la
cabeza de martillo con una velocidad angular de 12 rad/s, contando
que realizo el lanzamiento después de darle 10 voleos completos a la cabeza
del martillo.
Calcular el tiempo que le toma al atleta realizar el lanzamiento.

Solución:
Primer paso es identificar los datos que me brinda el problema, en este caso nos habla de un atleta
que hace un lanzamiento de una cabeza de martillo con una velocidad angular de 12 rad/s realizando 10 voleos. antes
de realizar el lanzamiento.
Un voleo es igual a una vuelta completa desde el punto de partida, una vuelta es igual a 2 π rad.
organizando los datos tenemos lo siguiente:
Desplazamiento angular = 10 * 2π = 62.83 rad
Velocidad angular = 12 rad/s
Ya teniendo los datos organizados, el problema nos pide calcular la el tiempo que le toma al atleta realizar el lanzamiento. Para este caso debemos usar una ecuación de la sección de formulas que me permita calcular el tiempo. Usaremos la siguiente formula:
t =
t =
= 5.24 segundos
Rta:El atleta le tomó 5.24 segundos en realizar el lanzamiento.
Ejemplo 3
Deicy se dirige hacia su casa, cuando llega quiere saber el tiempo que se demoró, para lo
cual mide la llanta de su bicicleta y obtiene 60 cm de
diámetro y su velocidad tangencial fue de 6 m/s.
Calcular el tiempo que le tomo a Deicy llegar a su casa, sabiendo que la rueda dio 1000 vueltas en el recorrido.

Solución:
Primer paso es identificar los datos que brinda el problema, en este caso habla de una bicicleta con
ruedas que cuyo diámetro es de 60cm
con una velocidad tangencial de 6 m/s y agrega que en todo el
recorrido la rueda de la bicicleta dio 1000 vueltas.
En este caso hay que ordenar las unidades con respecto a las definidas por el sistema
Internacional.
Radio = diámetro / 2 = (60cm / 100) / 2 = 0.3 metros
Desplazamiento angular = 1000 vueltas * 2π = 6283.18 rad
Velocidad tangencial = 6 m/s
El segundo paso calcularemos la longitud de arco para esto es necesario buscar
una
ecuación en la sección de formulas que me permita calcular la
longitud de arco relacionando el desplazamiento angular y el radio, usaremos la siguiente ecuación:
L = θ * R
L = 6283.18 * 0.3 = 1884.95 metros
Teniendo como resultado una longitud de arco batido de 1884.95
metros
Al calcular la longitud de arco buscamos una formula que relacione la velocidad tangencial y la
longitud de
arco, para cual usaremos la siguiente ecuación:
t =
t =
= 314.16 segundos
RTA:Teniendo como resultado que Deicy se tardo
314.16 segundos en llegar a su casa.
Aplicaciones del Movimiento Circular Uniforme en la vida real
Existe un gran interés práctico en el estudio de los movimientos circulares y, en particular, el estudio de la MCU. Se convierte en una referencia para medir el tiempo al usar una cantidad de este movimiento (un segundo, un día o un año) como unidad de medida porque es un movimiento periódico que produce objetos cosmológicos. Por otro lado, existen varios artefactos manufacturados que tienen movimientos circulares y hacen uso de ellos, sean uniformes o no, incluyendo manecillas de reloj, satélites para comunicaciones, discos giratorios y otros medios, norias, ruedas y aviones.
Rotación de la tierra
El movimiento circular en que la tierra gira sobre si misma durante un periodo de tiempo de 24 horas.
En la rotación posee un aceleración centrípeta la cual hace que sus parte no salgan volando en todas
las direcciones.
Toca disco de vinilo
este posee un movimiento circular uniforme en el momento de su reproducción en el toca disco. Tiene
una fuerza centrípeta que hace que el disco se gire solo en un punto y con una velocidad constante.
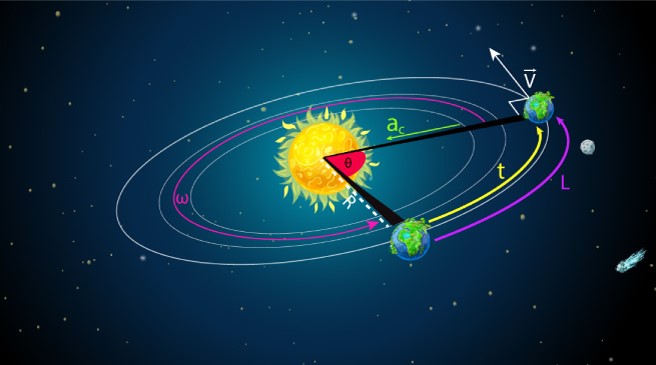
Traslación de la tierra
Movimiento circular en que la tierra se desplaza en órbita alrededor del sol durante un periodo de
tiempo de 365 días. En la traslación, en la tierra posee una aceleración centrípeta la cual hace que
la tierra no se salga de su órbita.
Principios históricos del Movimiento Circular Uniforme
Al igual que otros fenómenos físicos, la historia del movimiento circular se remonta a los antiguos
filósofos,
pensadores y científicos, incluidos Galileo, Newton, Copérnico y Aristóteles.
Cada uno de estos personajes hizo contribuciones significativas a las causas fundamentales de estos
fenómenos físicos,
donde pudieron establecer las primeras leyes que los rigen a través del surgimiento de la mecánica
como una rama
separada de la física. El descubrimiento de estos movimientos fue la culminación de las
contribuciones de muchos
filósofos y científicos notables.