INICIO
ARTÍCULOS
CALCULADORAS
Articulo de MCUA
Movimiento Circular Uniforme Acelerado
Que es MCUA
El término "movimiento circular uniformemente acelerado" (m.c.u.a.) o "movimiento circular
uniformemente variado"
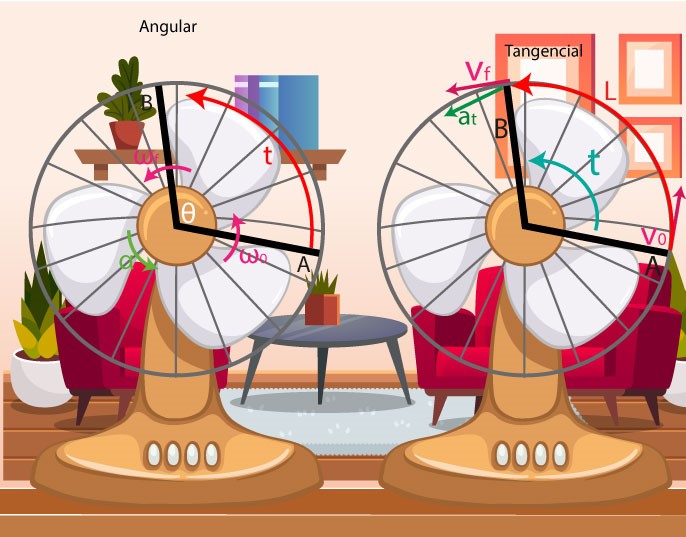
(m.c.u.v.) se refiere a un movimiento circular en el que la aceleración angular es constante.
Tiene un vector velocidad
que es perpendicular a la trayectoria en cada punto y varía uniformemente su módulo.
Estas son algunas características del Movimiento Circular Uniforme Acelerado:
- La aceleración tangencial es constante.
- La aceleración normal, cambia de dirección del vector velocidad. Siendo no constante ya que varia en base a la velocidad en un punto en concreto.
- La velocidad angular varia de forma uniforme.
Indice
Fórmulas despejadas angulares del Movimiento Circular Uniforme Acelerado (MCUA)
Desplazamiento angular
θ = ω0 * t +
12
* α * t²
θ = ωf * t -
12
* α * t²
θ =
ω0 +
ωf2
* t
θ =
ωf² -
ω0²2 * α
Velocidad angular inicial
ω0 = ωf - α * t
ω0 = √(ωf² - 2 * α * θ )
ω0 = 2 *
θt
- ωf
ω0 =
θt
- 0.5 * α * t
Velocidad angular final
ωf = 2 *
θt
- ωi
ωf = ω0 + α * t
ωf = √(ω0² + 2 *α *θ )
ωf =
θt
+ 0.5 * α * t
Tiempo
t =
ωf -
viα
t =
2 *
θωi + ωf
t =
-
ω0 + √(ω0²
- 4*(α / 2) *
(- θ))
2*(α / 2)
t =
ωf - √(
ωf² +
4 * (α / 2) * (-
θ))
2 * (α / 2)
Aceleración Angular
α =
ωf -
ω0t
- ωi
α =
θ - (
ω0 * t)
0.5 * t²
α =
ωf² - ω0²
2 * θ
α = -
θ - (
ωf * t)
0.5 * t²
ωf: Es la velocidad angular final (rad/s)
ω0: Es la velocidad angular inicial (rad/s).
α: Es la aceleración angular (rad/s)².
t: Es el tiempo (s).
θ: Es el desplazamiento angular (rad).
Fórmulas tangenciales del Movimiento Circular Uniforme Acelerado (MCUA)
Longitud de arco
L = v0 * t +
12
* at * t²
L = vf * t -
12
* at * t²
L =
v0 +
vf2
* t
L =
vf² -
v0²2 * at
Velocidad Tangencial inicial
v0 = vf - at * t
v0 = √(vf² - 2 * at * L )
v0 = 2 *
Lt
- vf
v0 =
Lt
- 0.5 * at * t
Velocidad Tangencial final
vf = 2 *
Lt
- vi
vf = v0 + at * t
vf = √(v0² + 2 *at *L )
vf =
Lt
+ 0.5 * at * t
Tiempo
t =
vf -
viat
t =
2 *
Lvi + vf
t =
-
v0 + √(v0²
- 4*(at / 2) *
(- L))
2*(at
/ 2)
t =
vf - √(
vf² +
4 * (at / 2) * (-
L))
2 * (at / 2)
Aceleración Tangencial
at =
vf -
v0t
- vi
at =
L - (
v0 * t)
0.5 * t²
at =
vf² - v0²
2
* L
at = -
L - (
vf * t)
0.5 * t²
vf: Es la velocidad tangencial final (m/s)
v0: Es la velocidad tangencial inicial (m/s).
at: Es la aceleración tangencial (m/s)².
t: Es el tiempo (s).
L: Es longitud de arco (m).
Formulas auxiliares
ac =
v²R
= ω² * R
L= R * θ
v= ω * R
at = α * R
R: Radio (m)
ac: Aceleración centrípeta (m/s²).
Gráficas de MCUA - MCUV
El movimiento circular uniforme acelerado (MCUA) o movimiento circular variado
(MCUV)es un movimiento circular que durante todo el recorrido,
pero la velocidad no es constante debido a la aceleración.
Posición
La inclinación de la parábola de la gráfica depende de la velocidad. A mayor pendiente,
mayor
velocidad.
La ecuación de la posición de un cuerpo en el instante t es la siguiente:
x(t) = x0 + ω0 * t + 1/2 * α *
t²
siendo x0 la posición inicial, ω0 la velocidad inicial,
α la aceleración, y la t el tiempo.
Velocidad
La velocidad se ve afectada por la aceleración, al realizar la ecuación el resultado es una
recta ascendente o descendente.
La velocidad en MCUA puede ser positiva o negativa, depende del signo que acompañe la
velocidad definirá la dirección del cuerpo.
La gráfica de velocidad en base al tiempo se expresa con la siguiente ecuación:
v = ω0 + α * t
donde ω0 es la velocidad angular inicial, a es la
aceleración y t es
el tiempo.
Aceleración
La aceleración en MCUA es constante, siendo representado en el plano cartesiano como una
recta,
la aceleración debe ser diferente de cero para que el movimiento sea considera movimiento
circular uniforme acelerado.
Siendo representada con la siguiente ecuación:
a = cte
donde a es aceleración y cte es constante.
Ejemplos de Movimiento Circular Uniforme Acelerado
A continuación se podrá ver ejemplos clásicos del Movimiento Circular Uniforme Acelerado teniendo
en cuenta
que todos estos escenarios son en un mundo ideal donde la fricción no afecta el movimiento, asi
haciendo hincapié en la velocidad es variable y la aceleración es constante.
Ejemplo 1
Un motociclista parte del reposo con una aceleración constante de 4 m/s²
.
Calcular la longitud de arco y la velocidad tangencial final a los 10
segundos
de la rueda.
Solución:
El problema nos habla de un motociclista parte del reposo con una aceleración de 4 m/s² y añade un tiempo de 10 segundos.
Velocidad inicial = 0 m/s
tiempo = 10 segundos
Aceleración tangencial = 4 m/s²
Ya teniendo los datos organizados, el problema nos pide calcular la longitud de arco, en este paso se debe buscar entre las formulas una que nos permita hallar la longitud de arco en la sección de formulas una ecuación que no involucre la velocidad final ya que no la conocemos.
L = v0 * t +
12
* at * t²
L = 0 * 10 +
12
* 4 * 10²
Teniendo como resultado una longitud de arco de 200 metros.
La segunda parte nos pide calcular la velocidad tangencial final, por lo cual usaremos la siguiente
ecuación:
vf = 2 *
Lt
- vi
vf = 2 *
20010
- 0
= 40 m/s
Rta: La longitud de arco recorrida por la rueda en 10 segundos es de 200 metros y alcanzó una velocidad final de 40 m/s.
Ejemplo 2
Un helicóptero parte del reposo y alcanza una velocidad de 60
rad/s en su rotor y un tiempo de 25 segundos.
Calcular el angulo de desplazamiento barrido y la aceleración angular del rotor.
Solución:
Primer paso es identificar los datos que me brinda el problema, en este caso nos habla de un helicóptero con velocidad final de 60 rad/s que alcanza en un tiempo de 25 segundos.
organizando los datos tenemos lo siguiente:
Velocidad final = 60 rad/s
Tiempo = 25 segundos
Velocidad inicial = 0 rad/s
Ya teniendo los datos organizados, el problema nos pide calcular el angulo de desplazamiento. Para este caso debemos usar una ecuación de la sección de formulas que no use la aceleración angular ya que no la conocemos.
θ =
ω0 +
ωf2
* t
θ =
0 +
602
* 25
= 750 rad
Teniendo como resultado un desplazamiento angular de 750 rad.
Para la segunda parte nos pide calcular la aceleración angular, para ellos usaremos la siguiente
ecuación:
α =
θ - (
ω0 * t)
0.5 *
t²
α =
750 - (
0 * 25)
0.5 *
25²
= 2.4 rad/s².
Rta:El desplazamiento angular del rotor fue de 750 rad con una aceleración angular constante de 2.4 rad/s².
Ejemplo 3
Un generador eólico hace un desplazamiento angular de 1800 rad
partiendo del reposo para
lo cual le toma 60 segundos en alcanzar su velocidad máxima,
sabiendo
que las
aletas del generador miden 2 metros.
Calcular la longitud de arco y la aceleración tangencial.
Solución:
Primer paso es identificar los datos que brinda el problema, en este caso habla de un generador
eólico que le toma 60 segundos
en alcanzar su velocidad
máxima y su desplazamiento angular en ese tiempo es de 1800 rad y
el radio es de 2 metros.
Radio = 2 metros
Desplazamiento angular = 1800 rad
Tiempo = 60 segundos
Velocidad inicial = 0
El segundo paso calcularemos la longitud, para esto es necesario buscar una
ecuación en la sección de formulas que relacione el radio con
desplazamiento angular, usaremos la siguiente ecuación:
L = R * θ.
L = 2 * 1800 = 3600 metros
Teniendo como resultado la longitud de arco batido de 3600
metros.
Para el ultimo paso calcularemos la aceleración tangencial de aterrizaje para lo cual usaremos la
siguiente
ecuación:
at =
L - (
v0 * t)
0.5 *
t²
at =
3600 - (
0 * 60)
0.5 *
60²
= 2 m/s²
RTA:Teniendo como resultado que el generador eólico le toma una longitud de arco de 3600 metros con una aceleración tangencial constante de 2 m/s² para alcanzar su velocidad máxima.
Aplicaciones del Movimiento Circular Uniforme Acelerado en la vida real
El Movimiento Rectilíneo Uniforme Acelerado es uno de los temas que trata la física mecánica en el
tema de
cinemática.
Este tema describe el movimiento de un objeto que presenta una trayectoria circular, aumentando o
disminuyendo la velocidad de forma constante a medida que transcurre el tiempo.
Ruedas
Todos los vehículos terrestres tienen ruedas que presentan un movimiento circular uniforme acelerado
o desacelerado ya que su velocidad aumenta y disminuye.
Las hélices de un helicóptero
Las hélices giran con un movimiento circular uniforme y su velocidad varia en base a la aceleración.
Ventilador
Las hélices giran con un movimiento circular uniforme acelerado cuando es encendido y cuando llega a
su velocidad final gira con velocidad constante y una aceleración de cero.
Principios históricos del Movimiento Circular Uniforme Acelerado
Al igual que otros fenómenos físicos, la historia del movimiento circular se remonta a los antiguos filósofos, pensadores y científicos, incluidos Galileo, Newton, Copérnico y Aristóteles. Cada uno de estos personajes hizo contribuciones significativas a las causas fundamentales de estos fenómenos físicos, donde pudieron establecer las primeras leyes que los rigen a través del surgimiento de la mecánica como una rama separada de la física. El descubrimiento de estos movimientos fue la culminación de las contribuciones de muchos filósofos y científicos notables.