inicio INICIO ARTICULOS ARTÍCULOS CALCULADORAS CALCULADORAS

Articulo de MPCL

Movimiento Parabólico de Caída Libre

Que es el movimiento parabólico

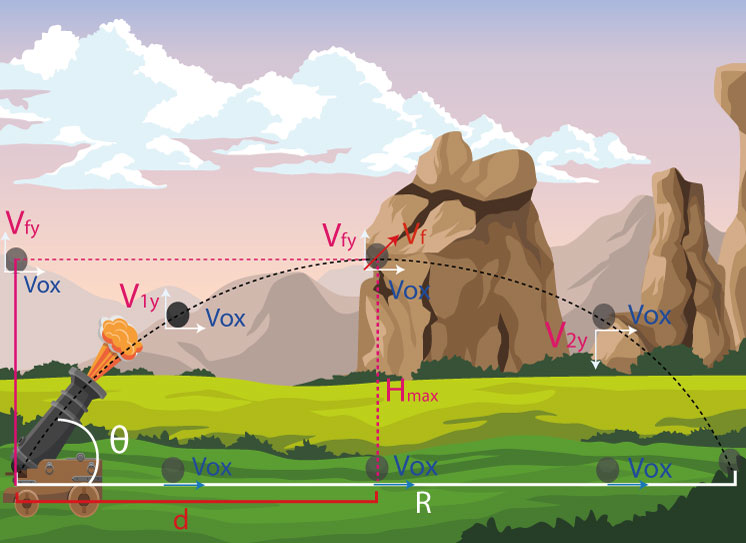
Un movimiento en el que una parte del cuerpo realiza una trayectoria parabólica se conoce como movimiento parabólico. Esta trayectoria es un movimiento ideal de un objeto que se mueve sin encontrar resistencia del medio mientras está sujeto a un campo gravitatorio homogéneo. El movimiento parabólico puede entenderse como una composición de dos movimientos rectilíneos, uno uniformemente horizontal y otro uniformemente acelerado verticalmente.

Estas son algunas características del movimiento parabólico:

  • El angulo de salida es igual al angulo de llegada.
  • Se requiere un ángulo de salida de 45° para lograr la mayor distancia de alcance posible.
  • Una vez establecido el ángulo inicial, el factor que más afecta a la distancia recorrida es la velocidad..
  • Conocer la velocidad, el ángulo de inclinación inicial (en la salida) y la diferencia de altura entre los puntos de salida y llegada es todo lo que se necesita para reproducir la trayectoria completa.

Indice

Fórmulas despejadas de Movimiento parabólico

Velocidad inicial

v0 = √(

2 * g * h/sen(θ)²

)

v0 =

g * tvuelo/2 * sen(θ)

v0 = √(

g * R/sen(2 * θ)

)

v0 = √( v0x² + v0y²)

Velocidad inicial x

v0x = v0 * cos(θ)

v0x =

d/t

v0x = √( v0² - v0y² )

Velocidad inicial y

v0y = v0* sen(θ)

v0y = vfy* g * t

v0y =

2 * h/t

- vfy

v0y =√(vfy - 2 * g * h)

Tiempo

t =

vfy + v0y /g

t =

v0y + √( v0y² -2 * g * h) / g

t =

2 * h/v0y

t =

d/v0x

Altura

h =

v0y + vfy/2

* t

h =

vfy² + v0y² / 2 * g

h =

v0² * sen(θ)² /2 * g

Formulas adicionales

R =

v0² * sen(2 * θ) / g

tvuelo =

2 * v0 * sen(θ) /g

d = v0x * t

v0:velocidad inicial.

v0x: velocidad inicial en el eje x (componente horizontal).

v0y:velocidad inicial en el eje y (componente vertical).

vfy:velocidad final en el eje y (componente vertical), La velocidad final en y es igual a 0.

d: distancia recorrida en el eje x.

g: Es la aceleración o la gravedad constante.

t: tiempo.

t vuelo: tiempo total de vuelo.

R: alcance horizontal.

θ: angulo del vector inicial.

Gráficas del movimiento movimiento parabólico de caída libre

El movimiento de caída libre es un movimiento en linea recta que durante todo el recorrido, pero la velocidad no es constante debido a la gravedad.

Posición en y


La posición con respecto al eje y es una parábola que parte desde una altura y al llegar a su altura máxima desciende hasta su altura inicial. Lo cual se puede dividir en dos movimientos, siendo el tiro vertical hasta su altura máxima y en su descenso desde la altura máxima un movimiento de caída libre.
La ecuación de la posición de un cuerpo en el instante t es la siguiente:

y(t) = h0 + v0 * t * sen(θ) - 1/2 * g * t²
siendo h0 la altura inicial, v0 la velocidad inicial, g la gravedad, y la t el tiempo.

Posición en x


La posición en el eje x es representada por una pendiente ya que su velocidad es constante, haciendo referencia que el movimiento en el eje x es un movimiento rectilíneo uniforme. La gráfica de la posición en base al tiempo se expresa con la siguiente ecuación:

x = v0 * t * cos(θ)
donde v0 es la velocidad inicial, t es el tiempo y θ es el angulo de tiro.

velocidad en x


La velocidad en el eje x es constante, haciendo referencia a que la velocidad en el eje x es puede ser representada como un movimiento rectilíneo uniforme. La gráfica de velocidad en base al tiempo se expresa con la siguiente ecuación:

vx = v0 * cos(θ)
donde v0 es la velocidad inicial y θ es el angulo de tiro.

Velocidad en y


La velocidad en el eje es afectada por la gravedad, dividiendo la velocidad en dos movimientos: Siendo un movimiento de tiro vertical hasta su altura máxima y un movimiento de caída libre en su descenso.
Siendo representada con la siguiente ecuación:

vy = v0 * sen(θ) - g * t
donde g es la gravedad, v0 es la velocidad inicial, t es el tiempo y θ es el angulo de tiro.

Aceleración


La aceleración o gravedad es constante, siendo representado en el plano cartesiano como una recta, la aceleración equivale a 9.8 m/s²
Siendo representada con la siguiente ecuación:

a = cte
donde a es aceleración y cte es constante.

Ejemplos de Movimiento parabólico de de caída libre

A continuación se podrá ver ejemplos clásicos de movimiento parabólico teniendo en cuenta que todos estos escenarios son en un mundo ideal donde la fricción no afecta el movimiento, asi haciendo hincapié en que la gravedad es constante.

Ejemplo 1

Un futbolista patea una pelota con una velocidad inicial de 20 m/s , donde la pelota sale disparada con un angulo de30°.
Calcular la altura máxima y el alcance horizontal.

Solución:

El problema una pelota disparada con una velocidad inicial de 20 m/s con un angulo de disparo de 60°.


Gravedad = 9.8
v0 = 20m/s
θ = 30°.

Ya teniendo los datos organizados, el problema nos pide calcular la altura máxima que alcanzara la pelota para ello buscaremos una formula en la sección de formulas ,que nos permita calcular la altura máxima, para lo cual usaremos la siguiente.


h =

v0² * sen(θ)² /2 * g

h =

20² * sen(30)² /2 * 9.8

Teniendo como resultado una alturas máxima de 5.10 metros.

La segunda parte nos pide calcular el alcance horizontal para lo cual usaremos la siguiente formula:


R =

v0² * sen(2 * θ) / g

R =

20² * sen(2 * 30) / 9.8

= 35.34 metros.


Rta: La pelota alcanzara una altura máxima de 5.10 metros recorrerá un alcance horizontal de 35.34 metros.




Ejemplo 2

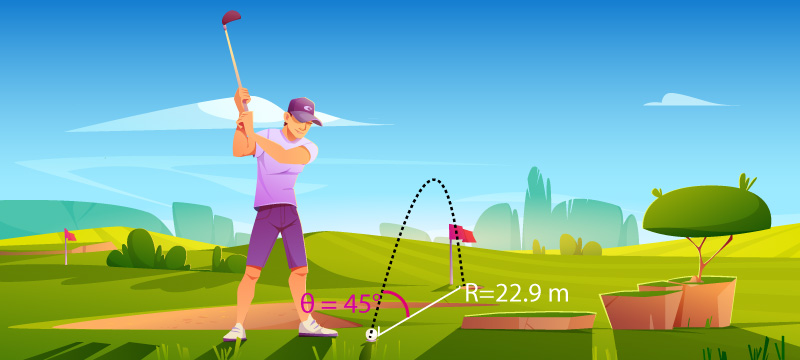
Una pelota de golf es golpeada con un angulo de ataque de 45° teniendo en cuenta que la distancia entre la pelota y el hoyo es de 22.9 metros
Calcular la velocidad inicial y el tiempo total de vuelo.

Solución:

Primer paso es identificar los datos que me brinda el problema, en este caso nos habla de una pelota de golf que es disparada con un angulo de 45°, que recorre una distancia de 22.9 metros y se asume que el valor de la aceleración o gravedad es de 9.8 m/s². organizando los datos tenemos lo siguiente:

Aceleración = 9.8 m/s²
Angulo = 45°
Alcance horizontal = 22.9 metros


Ya teniendo los datos organizados, el problema nos pide calcular la velocidad inicial, para este caso debemos usar una ecuación de la sección de formulas que permita calcular la velocidad inicial, para lo cual usaremos la siguiente ecuación:.



v0 = √(

g * R/sen(2 * θ)

)


v0 = √(

9.8 * 22.9/sen(2 * 45)

)


= 14.9 m/s

Teniendo como resultado una velocidad inicial de 176.4 metros.


En el segundo paso calcularemos el tiempo total de vuelo, para lo cual usaremos la siguiente ecuación:

tvuelo =

2 * v0 * sen(θ) /g

tvuelo =

2 * 14.9 * sen(45) /9.8

= 2.1 segundos


RTA:La pelota de golf fue disparada con una velocidad inicial de 14.9 m/s, tomándole en un tiempo de 2.1 segundos.




Ejemplo 3

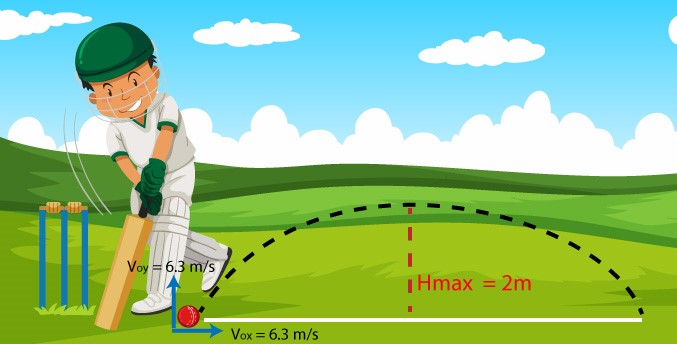
Un bateador golpea una pelota de cricket con una velocidad inicial en el eje x y el eje y de 6.3 m/s alcanzando una altura máxima de 2 metros.
Calcular la velocidad inicial y el tiempo que le tomo alcanzar la altura máxima.

Solución:

Primer paso es identificar los datos que brinda el problema, en este caso habla de una bola de cricket que es disparada con una velocidad en el eje x y en el eje y de 6.3 m/s , una altura máxima de 2 metros y se asume una aceleración o gravedad de 9.8 m/s².

velocidad inicial en x = 6.3 m/s
velocidad inicial en y = 6.3 m/s
Altura máxima = 2 metros
gravedad = 9.8 m/s²

El segundo paso calcularemos la velocidad inicial, para esto es necesario buscar una ecuación en la sección de formulas que me permita calcular la velocidad inicial para lo cual usaremos la siguiente ecuación:

v0 = √( v0x² + v0y²)


v0 = √( 6.3² + 6.3²) = 9 m/s


Teniendo como resultado una velocidad inicial de 9 metros,

Para el ultimo paso calcularemos el tiempo el tiempo que le toma alcanzar la altura máxima para lo cual usaremos la siguiente ecuación:

t =

2 * h/v0y

t =

2 * 2/6.3

= 0.64 segundos.



RTA:Teniendo como resultado que la pelota fue bateada con una velocidad inicial de 9 m/s y le tomo un tiempo de 0.64 segundos en alcanzar la altura máxima.

Aplicaciones del Movimiento parabólico de caída libre en la vida real

El movimiento parabólico se define como la combinación simultánea de dos movimientos distintos: un desplazamiento horizontal uniforme y un movimiento vertical acelerado. Es una propiedad de un objeto o proyectil que está sujeto a las leyes de un campo gravitatorio uniforme y se mueve a través de un espacio con poca o ninguna resistencia.

Algunas de sus aplicaciones son las siguientes:

  • El disparo de un proyectil militar (carga de artillería, mortero, etc.). Desde el cilindro del cañón hasta el punto de caída u objetivo.
  • El disparo de un balón de fútbol. Desde la arquería hasta caer en el campo contrario.
  • El lanzamiento de una bomba o misil. Desde un avión en pleno vuelo es un movimiento semiparabólico pues cursa la mitad de una parábola
  • La trayectoria de una pelota de golf. Durante el tiro inicial de larga distancia.

Principios históricos del movimiento parabólico de caída libre

El hombre conocía las trayectorias parabólicas pero no se refería a ellas como tales, y venía experimentando con armas parabólicas desde el principio de los tiempos. El movimiento parabólico ha sido ampliamente investigado desde la antigüedad, como lo demuestra su inclusión en los primeros libros de texto de balística con el objetivo de aumentar la precisión en el lanzamiento de proyectiles.

En cuanto al movimiento de las estructuras cercanas a la superficie de la tierra, Aristóteles (384 aC en Estagira, Macedonia - 322 aC en Calcis Eubea, Grecia) afirmó que "una piedra permanece en reposo o se mueve en línea recta hacia el centro de la tierra a menos que parezca estar sujeta a una fuerza externa".

Sin embargo, las bases de su conocimiento no se establecieron hasta que Galileo Galilei (15 de febrero de 1564 en Pisa - 8 de enero de 1642 en Arcetri, cerca de Florencia) explicó las leyes que rigen el movimiento.

Galileo analizó el movimiento parabólico representado en la Figura como la superposición de dos fuerzas: una era la tendencia natural del cuerpo a mantener el movimiento (la Ley de Inercia), lo que significaba que incluso después de dejar el borde de la mesa, el cuerpo continuaría moviéndose horizontalmente . La otra fuerza era la caída libre. Estos movimientos se producen simultáneamente y dan lugar al movimiento parabólico (la curva que caracteriza a la primera pelota es una parábola). Galileo se convirtió en la primera persona en describir la trayectoria de un cuerpo humano independiente en dos dimensiones al hacer esto.