inicio INICIO ARTICULOS ARTÍCULOS CALCULADORAS CALCULADORAS

Articulo de MRUA

Movimiento Rectilíneo Uniforme Acelerado

Que es mrua

Como su nombre lo sugiere, el "Movimiento Rectilíneo Uniforme Acelerado (MRUA)" es el tipo de movimiento que se produce cuando se acelera un móvil. La aceleración se define como "el cambio de velocidad" durante un cierto período de tiempo, por lo que siempre hay un movimiento acelerado.

Estas son algunas características del Movimiento Rectilíneo Uniforme Acelerado:

  • La trayectoria es en linea recta, no cambia la dirección de la velocidad.
  • La velocidad cambia constantemente en relación a la aceleración, la velocidad aumenta o disminuye dependiendo si la aceleración es positiva o negativa.
  • La aceleración es diferente de cero.

Indice

Fórmulas del Movimiento Rectilíneo Uniforme Acelerado (mrua)

Distancia

d = v0 * t +

1/2

* a * t²

d = vf * t -

1/2

* a * t²

d =

v0 + vf/2

* t

d =

vf² - v0²/2 * a

Velocidad inicial

v0 = vf - a * t

v0 = √(vf² - 2 * a * d )

v0 = 2 *

d/t

- vf

v0 =

d/t

- 0.5 * a * t

Velocidad final

vf = 2 *

d/t

- vi

vf = v0 + a * t

vf = √(v0² + 2 * a * d )

vf =

d/t

+ 0.5 * a * t

Tiempo

t =

vf - vi/a

t =

2 * d/vi + vf

t =

- v0 + √( v0² - 4 * (a / 2) * (- d) ) /2 * (a / 2)

t =

vf - √( vf² + 4 * (a / 2) * (- d) ) /2 * (a / 2)

Aceleración

a =

vf - v0/t

- vi

a =

d - ( v0 * t) /0.5 * t²

a =

vf² - v0² /2 * d

a = -

d - ( vf * t) /0.5 * t²

vf: Es la velocidad final, es la velocidad al final de movimiento.

v0: Es la velocidad inicial, velocidad con la que un cuerpo parte del punto inicial del movimiento.

a: Es la aceleración constante del cuerpo en el movimiento.

t: Es el tiempo que tarda un cuerpo en completar el movimiento.

d: Es la distancia recorrida durante el movimiento.


En el Sistema Internacional (S.I.) la unidad de la distancia es el metro (m), para la velocidad es el metro por segundo (m/s) para el tiempo se utiliza el segundo (s)y la aceleración utiliza el metro por segundo cuadrado (m/s²) .

Gráficas de MRUA O MRUV

El movimiento rectilíneo uniforme acelerado (MRUA) o movimiento rectilíneo variado (MRUV)es un movimiento en linea recta que durante todo el recorrido, pero la velocidad no es constante debido a la aceleración.

Posición


La inclinación de la parábola de la gráfica depende de la velocidad. A mayor pendiente, mayor velocidad.
La ecuación de la posición de un cuerpo en el instante t es la siguiente:

x(t) = x0 + v0 * t + 1/2 * a * t²
siendo x0 la posición inicial, v0 la velocidad inicial, a la aceleración, y la t el tiempo.

Velocidad


La velocidad se ve afectada por la aceleración, al realizar la ecuación el resultado es una recta ascendente o descendente. La velocidad en MRUA puede ser positiva o negativa, depende del signo que acompañe la velocidad definirá la dirección del cuerpo. La gráfica de velocidad en base al tiempo se expresa con la siguiente ecuación:

v = v0 + a * t
donde v0 es la velocidad inicial, a es la aceleración y t es el tiempo.

Aceleración


La aceleración en MRUA es constante, siendo representado en el plano cartesiano como una recta, la aceleración debe ser diferente de cero para que el movimiento sea considera movimiento rectilíneo uniforme acelerado.
Siendo representada con la siguiente ecuación:

a = cte
donde a es aceleración y cte es constante.

Ejemplos de Movimiento Rectilíneo Uniforme Acelerado

A continuación se podrá ver ejemplos clásicos del Movimiento Rectilíneo Uniforme Acelerado teniendo en cuenta que todos estos escenarios son en un mundo ideal donde la fricción no afecta el movimiento, asi haciendo hincapié en la velocidad es variable y la aceleración es constante.

Ejemplo 1

Un tractor parte del reposo, se sabe que su velocidad máxima es de 20 m/s y el tiempo que le toma para alcanzar esa velocidad es de 10 segundos. Calcular la distancia que le toma al tractor acelerar a la velocidad máxima y su aceleración.

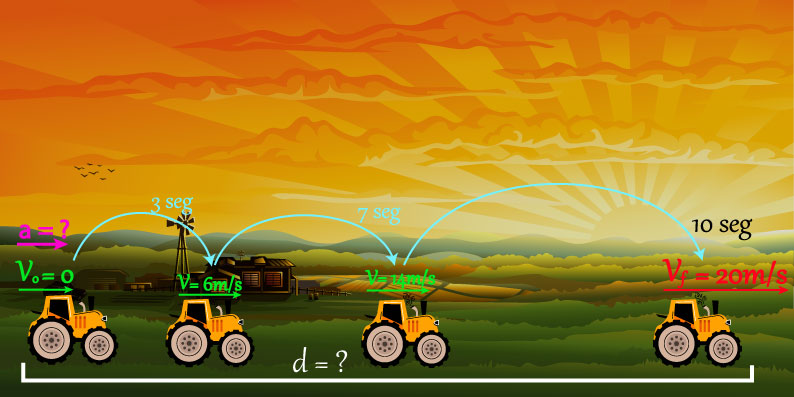
Solución:

El problema nos habla de un tractor con velocidad variable que parte del reposo con una velocidad de 0 m/s , su velocidad final es de 20 m/s y para alcanzar la velocidad final le toma 10 segundos.


Velocidad inicial = 0 m/s
Velocidad final = 20 m/s
tiempo = 10 segundos


Ya teniendo los datos organizados, el problema nos pide calcular la distancia que le toma acelerar hasta su velocidad máxima, en este paso se debe buscar entre las formulas una que nos permita hallar la distancia en la sección de formulas una ecuación que no involucre la aceleración ya que no se conoce.


d =

v0 + vf/2

* t

d =

0 + 20/2

* 10 = 100 metros

Teniendo como resultado una distancia de 100 metros

La segunda parte nos pide calcular la aceleración del tractor, por lo cual usaremos la siguiente ecuación:

a =

vf² - v0² /2 * d

a =

20² - 0² /2 * 100

= 2 m/s²


Rta: El tractor necesita 100 metros con una aceleración de 2 m/s² para obtener la velocidad máxima.




Ejemplo 2

Marta sale todos los días a correr, esta vez quiere medir el tiempo que le toma recorrer 200 metros.Sabiendo que Marta parte del reposo con una aceleración constante de 2 m/s².
Calcular el tiempo que le toma a Marta recorrer los 200 metros y cual fue velocidad al finalizar la prueba.

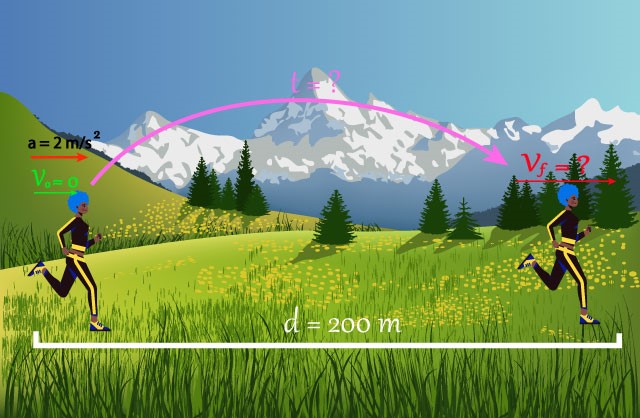
Solución:

Primer paso es identificar los datos que me brinda el problema, en este caso nos habla de una corredora que quiere recorrer 200 metros y que parte del reposo con una aceleración constante de 2 m/s².

organizando los datos tenemos lo siguiente:

Distancia = 200 metros
Aceleración = 2 m/s²
Velocidad inicial = 0 m/s


Ya teniendo los datos organizados, el problema nos pide calcular la el tiempo que le toma a Marta recorrer 200 metros. Para este caso debemos usar una ecuación de la sección de formulas que no use la velocidad final ya que no la conocemos.


t =

- v0 + √( v0² - 4 * (a / 2) * (- d) ) /2 * (a / 2)

t =

- 0 + √( 0² - 4 * (2 / 2) * (- 200) ) /2 * (2 / 2)

= 14.14 seg
Teniendo como resultado un tiempo de 14.14 segundos.

Para la segunda parte nos pide calcular la velocidad final, para ellos usaremos la siguiente ecuación:

Vf = v0- a * t
vf = 0 - 2 * 14.14 = 28.28 m/s


Rta:Marta tardo 14.14 segundos en recorrer la prueba de 200 metros y obtuvo una velocidad final de 28.28 m/s.




Ejemplo 3

Un avión desciende a la pista de aterrizaje con una velocidad de 400 km/h, se sabe que el avión recorre en el aterrizaje el 90 % de la pista, siendo la longitud de esta 2km.
Calcular la desaceleración del avión en el aterrizaje y el tiempo que le toma en detenerse.

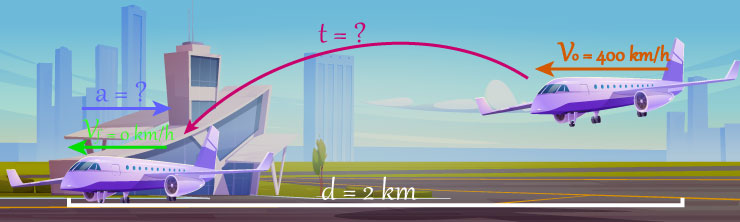
Solución:

Primer paso es identificar los datos que brinda el problema, en este caso habla de un aeronave que desciende con velocidad inicial de 400 km/h sobre una pista de aterrizaje de 2 km que solo recorre el 90% de la pista.
En este caso hay que ordenar las unidades con respecto a las definidas por el sistema Internacional.

velocidad inicial = 400 * 3.6 = 111.11 m/s
Distancia = 2 * 1000 = 2000 metros
Velocidad final = 0

Recordando el enunciado del problema nos dice que solo recorre el 90% de la pista, entonces tenemos lo siguiente:
Distancia = 2000 * 0.9 = 1800 metros

El segundo paso calcularemos la desaceleración en el aterrizaje, para esto es necesario buscar una ecuación en la sección de formulas que no use el tiempo, ya que no lo conocemos. Usaremos la siguiente formula:

a =

vf² - v0² /2 * d

a =

0² - 111.111² /2 * 1800

= - 3.429 m/s²

Teniendo como resultado una aceleración negativa de - 3.429 m/s², al ser la aceleración negativa nos indica una desaceleración.

Para el ultimo paso calcularemos el tiempo de aterrizaje para lo cual usaremos la siguiente ecuación:

t =

vf - vi/a

t =

0 - 111.111/-3.429

= 32.4 segundos



RTA:Teniendo como resultado que el avión tiene una desaceleración de - 3.429 m/s² y tarda en aterrizar 32.4 segundos.

Aplicaciones del Movimiento Rectilíneo Uniforme Acelerado en la vida real

El Movimiento Rectilíneo Uniforme Acelerado es uno de los temas que trata la física mecánica en el tema de cinemática.
Este tema es muy importante en la física ya que ayuda a describir el comportamiento de los cuerpos que se mueven en linea recta con velocidad variable con una velocidad constante, si bien este movimiento es uno de los fenómenos más simples, es la base para poder comprender muchos otros fenómenos físicos.

Aviación

En las pista de aterrizaje se presencia este fenómeno físico, ya que la pista de aterrizaje son rectas, cuando el avión aterriza con una velocidad empieza a variar su velocidad con respecto a su aceleración negativa, hasta que la velocidad final es cero.

Principios históricos del Movimiento Rectilíneo Uniforme Acelerado

El gran matemático Galileo Galilei, descubrió este movimiento mediante experimentos, como fueron dejando caer bolas desde pendientes y arrojando objetos desde la torre de pizza. Fue una teoría muy criticada y difícil de aceptar ya que existía una teoría de caída libre escrita por Aristóteles que era duramente criticada pero a su vez era apoyada por la iglesia lo que ocasionó muchas discusiones con Galilei, siendo tildado de hereje por la santa inquisición.

Es interesante y al mismo tiempo curioso notar cómo Galileo explicó por qué los aumentos de velocidad eran iguales: "porque cuando yo observo que una piedra al descender de una altura, partiendo del reposo, adquiere continuamente nuevos incrementos de velocidad, ¿Por qué no he de creer que tales aditamentos se efectúan según el modo más simple y más obvio para todos? Porque si observamos con atención, ningún aditamento, ningún incremento hallaremos más simple que aquel que se sobre añade siempre del mismo modo". Como dijo Galileo, los incrementos de velocidad son para intervalos iguales de tiempo. En el caso de MRUA, los intervalos de tiempo iguales son siempre iguales, como se muestra aplicando la ecuación de MRUA a intervalos de tiempo iguales y utilizando la velocidad del final del intervalo anterior como velocidad inicial.